Zoom H2 and H2n

Zoom H2n recorder

The Zoom H2n is a light, compact, and highly portable recorder with five microphone capsules on the top which records onto an SD card in WAV or MP3 format.  It can be used to record XY signals from one side or MS signals from the other (two of the microphone capsules are back-to-back cardioids generating the equivalent of a figure of 8 capsule).  Additionally, four channel (quad) surround can be recorded.  It can also be used to record from a remote source via a line in socket - but this is less interesting.

So far, so good - but what makes this device especially interesting is that there is an official firmware update available for it which generates ambisonic output.  This is horizontal-only, of course.  The format used is not the traditional "FuMa" B-format, but the Ambix (ACN/SN3D) format required by modern VR software such as Google Jump or YouTube 360, which makes the motivation for this obvious.  My H2n has been updated with this, of course (note that no other facilities are lost).

Modified versions of this device have also been made as part of the Brahma project.  One version had a socket on the top to hold a separate Brahma microphone, and the other had the Brahma microphone built-in at the top of the recorder.  Although I have a Brahma microphone, I do not have a modified H2n.

Zoom H2 recorder

The Zoom H2 was the direct predecessor of the H2n.  It is a pocket-sized recorder with four microphone capsules on top.  These are arranged as two pointing forwards at 90 degrees apart, and two facing backwards separated by 120 degrees.  Recordings are saved onto an SD card.  The device can record a stereo file from either the front or the rear capsule pair, or their combination, or it can record both pairs into two stereo files simultaneously for quad surround.  It also has a range of sample rates available.  An intriguing aspect is that it only has three spot settings for the sensitivity (a continuous level control that appears to be available is only a digital gain after the ADC, and so has no influence on clipping).  The device will only write 2GB files; longer recordings can be made, and the device will swap to a new file - a recent firmware update added buffering so that there is no gap between successive files.

H2 Quad to B-format

It was a rather obvious question whether we could make use of the H2 to record horizontal B-format, or rather, whether we could extract horizontal B-format from its quad output.  I decided to try, but my approach was thoroughly simplistic: I just assumed that the capsules are perfectly coincident, and that they are ideal cardioids.  Given these assumptions, it was quite easy to work out a combinations of sums and differences at varying levels that would cancel out the unwanted signals and leave each of the required components.  It would have been even easier if all the capsules were at right angles; it might even be worth trying to modify the device to make this so, for greater symmetry in particular - but I haven't.

A bit of Maths

Consider each cardioid Lf, Rf, Lb, and Rb, to be a perfect combination of an omni signal and a figure of 8 signal of the same level; assume they are coincident (this is already falling apart at about 5kHz). Simple trigonometry and the B-format definition show us that these correspond to B-format signals as follows:

Lf = W * sqrt(2) + X * cos(45) + Y * cos(45) = 1.414W + 0.707X + 0.707Y
Rf = W * sqrt(2) + X * cos(45) - Y * cos(45) = 1.414W + 0.707X - 0.707Y
Lb = W * sqrt(2) - X * cos(60) + Y * cos(30) = 1.414W - 0.5X + 0.866Y
Rb = W * sqrt(2) - X * cos(60) - Y * cos(30) = 1.414W - 0.5X - 0.866Y

We can cancel Y by summing left and right to give Front and Back:

F = Lf + Rf = 2*1.414W + 1.414X
B = Lb + Rb = 2*1.414W - X

So cancelling out the X and W terms in turn, we get:

W = (F / 1.414 + B) / (2 + 2*1.414)
X = (F - B) / (1.414 + 1)

To get Y, we can take the differences of the two microphone pairs, thus cancelling both W and X components, to give two sideways figure of eights consisting only of Y:

Yf = Lf - Rf = 1.414Y
Yb = Lb - Rb = 1.732Y

It is a matter of taste how one combines these to get a final consensus of the Y value; I give them equal weight, which means that the capsules pointing more to the sides contribute more - this seems fair:

Y = (Yf + Yb) / (1.414 + 1.732)

You can see these values (taken to a completely unjustified 6 decimal places) in the Plogue Bidule setup shown below (AudioMulch is not suitable for this, as it doesn't have the maths functions).

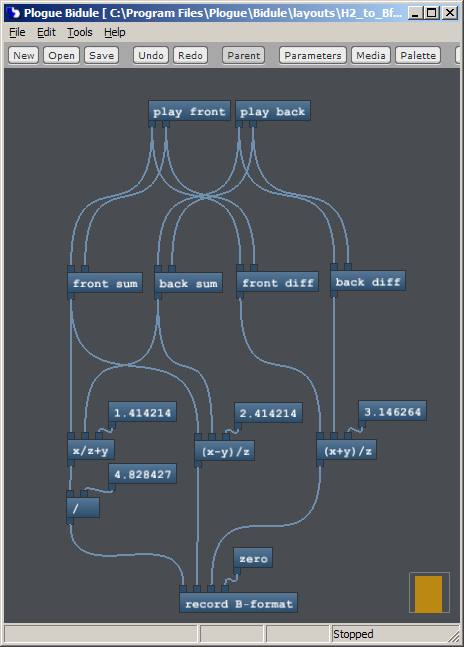
Results

What I wrote here originally was: "Actually, I won't bother with samples.  The results are poor.  You really do need to have well matched capsules in a more compact arrangement, and then calibrate them, for this to be worth considering."

However, Richard Furse has more recently (2014) checked my maths and tried this out with some success.  It is likely that my one test was inadequate, so I hope I didn't put too many people off the idea!